数据分析
商业智能(Business Intelligence,BI)、数据仓库(Data Warehouse,DW)和数据挖掘(Data Mining,DM)三者之间的关系:
数据仓库是一个集成、主题化、稳定的数据存储区域,为BI和DM提供数据支持。BI通过可视化分析和数据报表等方式,将数据转化为有价值的信息,帮助企业管理层和决策者快速准确地获得洞察,支持企业决策。而DM是从数据中自动提取模式、趋势和关系的过程,用于发现数据的隐含规律和预测未来走向
数据采集 -> 数据挖掘 -> 数据可视化
- 对于大数据:熵很小,使用数据挖掘算法
- 对于小数据:熵很大,了解背后规律
均值
平均值容易受到极端值的影响,只有在数据呈均匀分布或者正态分布的情况下才会有意义
辛普森悖论告诉我们,有的时候,在分组比较中占优势的一方,在总评中反而可能是失势的一方,平均值需要看它的分组构成,而不是简单地用平均值去代表所有的整体
大数定律与小数陷阱
- 大数定律:当随机事件发生的次数足够多(趋向无穷)时,发生的频率才会趋近于预期的概率
- 小数陷阱:每次的事件其实和上一次的事件是独立且随机的,某些事件在刚开始概率更高,并不意味着后面发生的概率会降低
期望值
反映在大数定律下多次执行某件事情之后,得到的一个最可能的收益结果
随机对照试验
通过多组随机试验来验证一个理论和假设是否真实,AB测试就是一种随机对照试验
直方图与幂分布
- 直方图是展示数据的分布,而柱状图是比较数据的大小
从直方图体现出来呈指数下降或者上升的分布形式,叫做“幂律分布”
帕累托法则:二八定律
拉普拉斯分布
跟正态分布相反,这种分布从左到右,斜率先缓慢增大再快速增大,到达最高点后变为负值继续先快速减小,最后再缓慢地减小
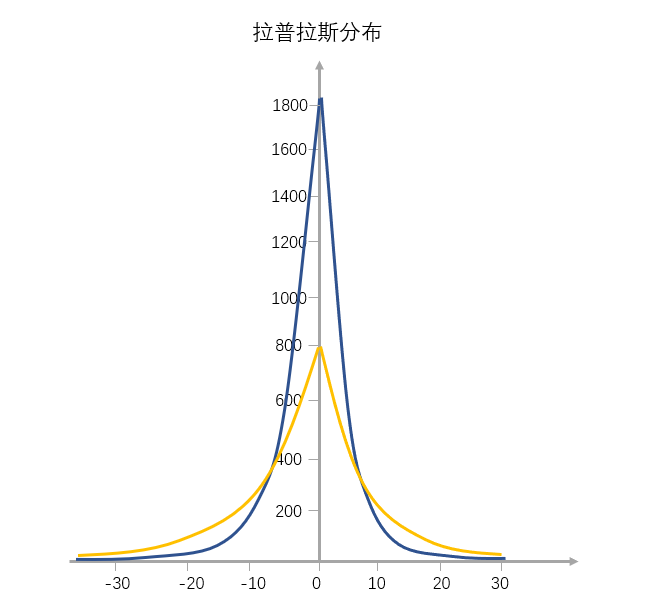
这种分布在资源导向的场景比较多见,比如股市、房价,越塔尖的个体越具有资源吸附能力
散点图与相关性
- 散点图反映的是两个变量之间的关系
- 为了能够明确展示数据之间的趋势,Y 轴必须要从零开始
- 为了表示趋势的清晰,一般都会添加一条趋势线来表明背后的规律
一些散点图的分布规律:
- 正相关、负相关
- 指数相关
- 正U分布和反U分布:当达到一定程度,资源投入越多、获得收益反而更少
- 无相关
- 更为复杂的情况
误区:
- 误判趋势:数据整体还不够完整,错误判断了这个数据的未来增长趋势
- 德克萨斯枪手谬误:数据是否代表了整体
- 幸存者偏差:在分析散点图的时候看到了规律,还要了解最终这个规律形成的原因和背后的场景
标准差
代表一组数值和平均值相比分散开来的程度。也就是说,标准差大代表大部分的数值和平均值差异比较大,标准差小代表这组数字比较接近平均值
标准误差代表一种推论的估计,它反映的是多次抽样当中样本均值之间的离散程度
数据抽样
小数据抽样:
- 简单随机抽样:从总体 N 个单位中随机地抽取 m 个单位作为样本,使得每一个样本被抽中的概率相同
- 系统抽样:依据一定的抽样距离,从整体中抽取样本,即限定每轮抽样的数据范围都不同
- 分层抽样:将抽样单位按某种特征或某种规则划分为不同的层,然后从不同的层中独立、随机地抽取样本,从而保证样本的结构接近于总体的结构
- 整群抽样:将总体中若干个单位合并为组(这样的组被称为群),抽样时直接抽取群,然后对所选群中的所有单位实施调查
分层抽样是先分层再从各层抽样本,整群抽样是先分群再抽一个群调查
大数据抽样:
- 蓄水池算法
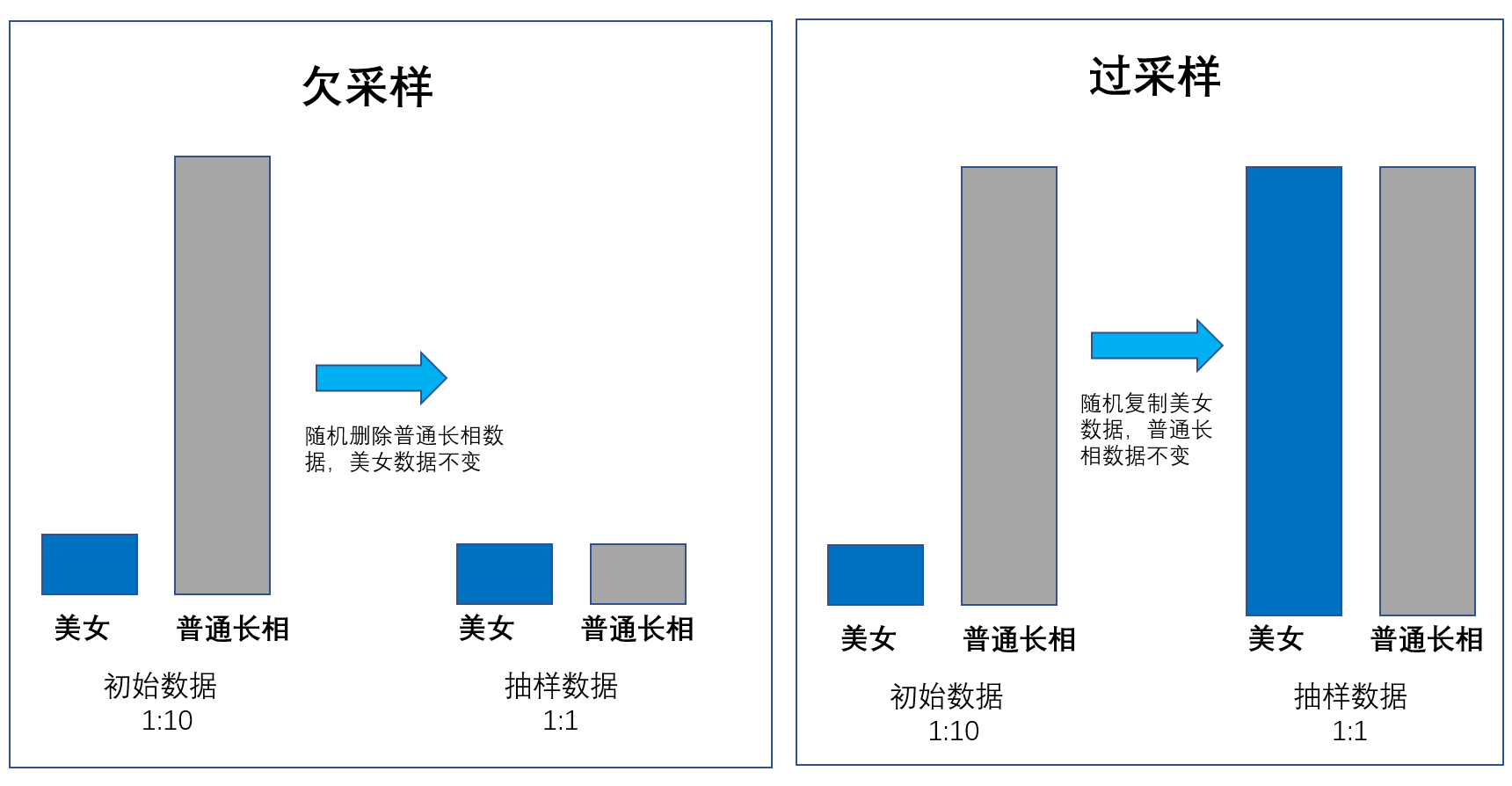
- 过采样
- 欠采样
public class ReservoirSampling {
private int[] ALL; // 整体的水池中的数据
private final int N = 100000; // 整体数据规模
private final int K = 1000; // 水池规模
private Random random = new Random();
public void setUp() throws Exception {
ALL = new int[N];
for (int i = 0; i < N; i++) {
ALL[i] = i;
}
}
private int[] Sampling(int K) {
int[] Pool = new int[K];
for (int i = 0; i < K; i++) { // 前面K条数据直接进入水池
Pool[i] = ALL[i];
}
for (int i = K; i < N; i++) { // K + 1个元素开始进行概率采样
int r = random.nextInt(i + 1); //这就是K/N的概率
if (r < K) {
Pool[r] = ALL[i]; //如果被选中了,那么这条数据就被从蓄水池中挤出来,新数据进去
}
}
return Pool;
}
}
指数
指数 = 变量值/标准值 x 100
指数公式本身很简单,关键在于指数公式的背后,要如何去制定一个能够保持指数有效性的规则
从股市上证沪深指数,到互联网用户忠诚指数,都需要定义解释一系列规则来创建这样的一个指数
要制定某个指数,比方说设定 KPI 的时候,我们要注意不要光看公式的建立,而是要把一系列定义调整的制度算法规定出来
因果倒置
数据的确是同步发生的,但是不代表这些数据之间有因果关系
精确率与置信区间
准确率 = 预测正确的样本数量 / 预测总的样本数量
精确率为预测正确的正例 (TP) 在所有预测为正例的样本中出现的概率
召回率用是预测正确的正例 (TP) 在原始的所有正例样本中出现的概率
置信度和置信区间是一组参数,说明算法模型误差有多大
回归
- 线性回归
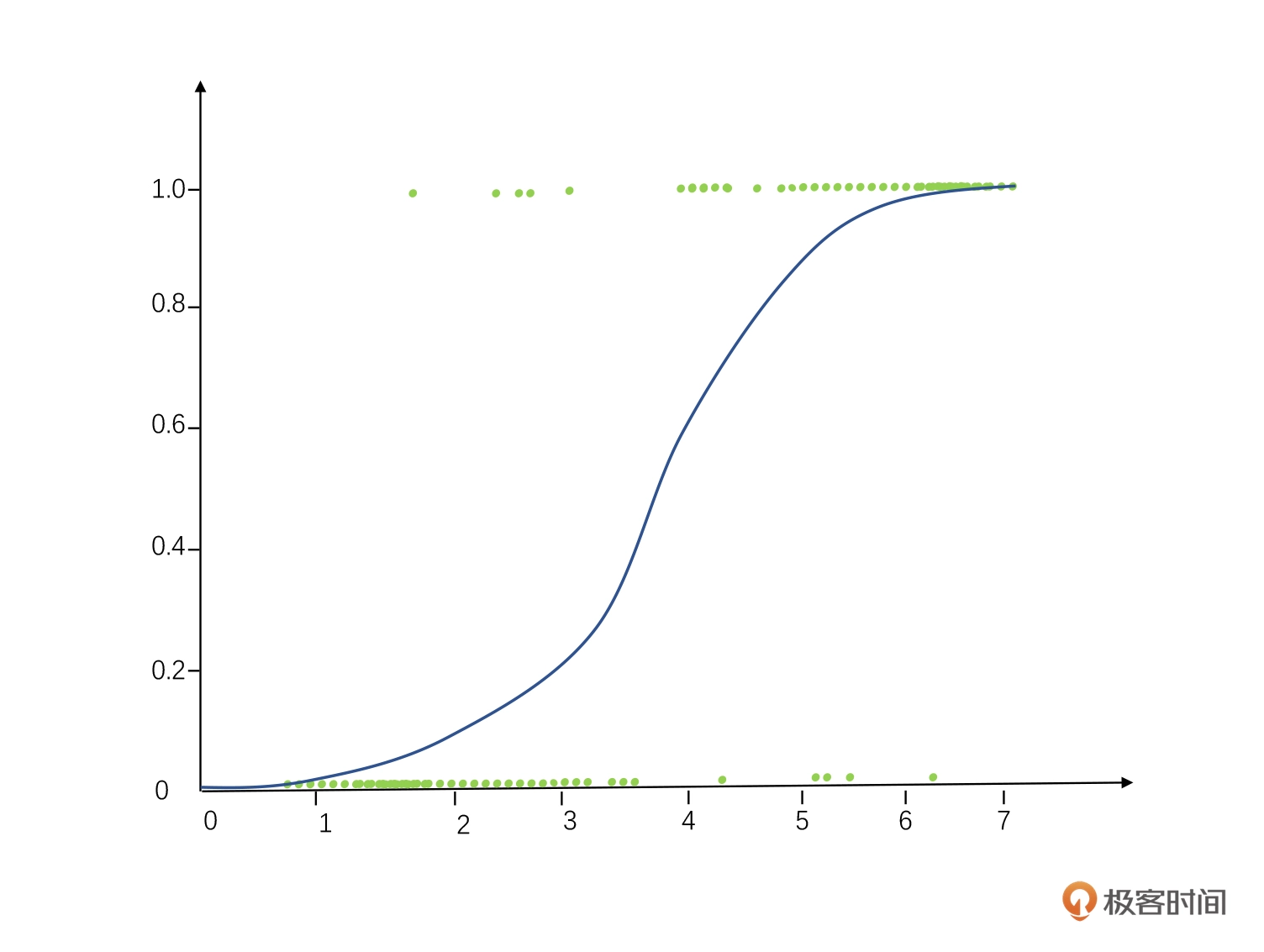
- 逻辑回归:广泛用于做分类问题,也就是把“成功 / 失败”“哪一种颜色”这类问题变成线性回归的样子
- 多项式回归:可能出现多个指数的数据,这种回归最佳拟合的线也不是直线,很可能是一个曲线
- 均值回归:实际发生的数据比理论上的预测更加接近平均值,整体趋势上会慢慢向一个平均值发展
两个变量之间有回归逻辑,不代表着两个变量之间有因果逻辑
关联规则
支持度(Support)
表示项集{X,Y}在总项集里出现的概率。表示A和B同时在总数I 中发生的概率:
Support(X→Y) = P(X,Y) / P(I) = P(X∩Y) / P(I) = num(X∩Y) / num(I)
置信度 (Confidence)
在先决条件X发生的情况下,由关联规则”X→Y“推出Y的概率。表示在发生X的项集中,同时会发生Y的可能性,即X和Y同时发生的个数占仅仅X发生个数的比例:
Confidence(X→Y) = P(Y|X) = P(X,Y) / P(X) = P(X∩Y) / P(X)
提升度(Lift)
表示含有X的条件下,同时含有Y的概率,与只看Y发生的概率之比。提升度反映了关联规则中的X与Y的相关性,提升度>1且越高表明正相关性越高,提升度<1且越低表明负相关性越高,提升度=1表明没有相关性,即相互独立
Lift(X→Y) = P(Y|X) / P(Y)
连坐算法
- Apriori 算法
如果 123 是频繁组合,则 12、13、23 也是频繁组合;若 12 是非频繁组合,则 123 也是非频繁组合
蒙特卡洛算法和拉斯维加斯算法
- 两类算法的统称,利用随机的方法来简化整体的算法过程
蒙特卡罗算法原理:每次计算都尽量尝试找更好的结果路径,但不保证是最好的结果路径。用这样寻找结果的方法,无论何时都会有结果出来,而且给的时间越多、尝试越多,最终会越近似最优解
拉斯维加斯算法原理:就是每次计算都尝试找到最好的答案,但不保证这次计算就能找到最好的答案,尝试次数越多,越有机会找到最优解
马尔可夫链
- 马尔可夫链蒙特卡罗算法(MCMC)
协同过滤
- 基于用户
- 基于物品
- 基于数据模型:基于样本的用户喜好信息,训练一个推荐模型,然后根据实时的用户喜好的信息进行预测,计算推荐
用数据说话
问题确定
和利益无关的问题都不值得做数据分析,值得的一个是带来更多的收入,一个是帮着节约成本
提出问题 -> 提出理想 -> 结构化分析
数据采集
- 一手数据:主要来自企业内部的大数据平台、数据仓库以及相关系统,还有部分数据来自用户访谈和调研问卷以及内部沉淀的历史文档
- 二手数据:是来自行业内的数据或者企业内二次加工过,有失真的可能
- 趋势分析法:找到某一个类型的数据之后,捕捉这个数据一个时间段以内的变化。通过这些数据变化,我们去知道曾经有哪些变化、对结果数据会有哪些影响,这样可以找到其中关键的问题和原因
- 快照扩展法:截取某个时点的情况,然后通过下钻的方式来扩展这个指标的分布情况。我们会看在这个时点里面我们各部分对于整体的占比和影响程度
- 衍生指标法:进一步进行数据的加工,制造出一些衍生指标来拨开迷雾,衍生指标就像几何当中的辅助线一样,会帮助我们看到更有意义的数据
数据揭示
- 讲好故事
实践
改变和创新的扩散过程是要有一个周期的,参考埃弗雷特·罗杰斯(E.M.Rogers)提出创新扩散模型
观点的认知到具体落实到行动,理性行为理论:一件事,从认知到行动意图,不但是有主观的个体认知,同时客观的世界也是一种规范作用
可视化
可视化图使用的情况:
- 分布
- 时间相关
- 局部/整体
- 偏差
- 相关性
- 排名
- 量级
- 地图
- 流动