线性代数
向量
向量(vector):也可以叫做矢量。它代表一组数字,并且这些数字是有序排列的
C++中的数组就叫做vector
向量可以用来表示某个物体的特征。其中,向量的每个元素就代表一维特征,而元素的值代表了相应特征的值,我们称这类向量为特征向量
向量空间
x1,x2,……,xn∈F,就有 Fn
假设 V 是 Fn 的非零子集,如果对任意的向量 x、向量 y∈V,都有 (x+y)∈V,我们称为 V 对向量的加法封闭;对任意的标量 k∈V,向量 x∈V,都有 kx 属于 V,我们称 V 对标量与向量的乘法封闭
如果 V 满足向量的加法和乘法封闭性,我们就称 V 是 F 上的向量空间
距离
可以把一个向量想象为 n 维空间中的一个点。而向量空间中两个向量的距离,就是这两个向量所对应的点之间的距离
- 曼哈顿距离
$$MD(x,y) = \sum_{i=1}^n |x_i - y_i|$$
- 欧氏距离
$$ED(x,y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^{2}}$$
- 切比雪夫距离
$$CD(x,y) = \argmax_1^n |x_i - y_i|$$
长度
通常使用欧氏距离来表示向量的长度
夹角
空间中两个向量所形成夹角的余弦值
$$Cosine(X,Y) = \frac{\sum_{i=1}^n (x_i * y_i)}{ \sqrt{\sum_{i=1}^n x^2 * \sum_{i=1}^n y^2}}$$
向量空间模型
向量空间模型假设所有的对象都可以转化为向量,然后使用向量间的距离,或者是向量间的夹角余弦来表示两个对象之间的相似程度
向量空间可以很形象地表示数据点之间的相似程度,不仅能运用在信息检索,也可以运用在基于相似度的一些机器学习算法中,例如 K 近邻(KNN)分类、K 均值(K-Means)聚类
信息检索:
- 将文档转为特征向量,分词后将词转换为向量,最简单的方法是用“1”表示这个词条出现在文档中,“0”表示没有出现,也可以对不同的词赋予不同的权重来丰富特征
- 将查询和文档进行匹配,查询需要先转为向量,因为查询与文档的维度不一样(出现的词),对于在文档出现而在查询没有出现的词,可以采取简单的置0,或者把文档的这个维度剔除掉
- 进行上面两个步骤后,就能得到每篇文档与查询的相似度了
运算
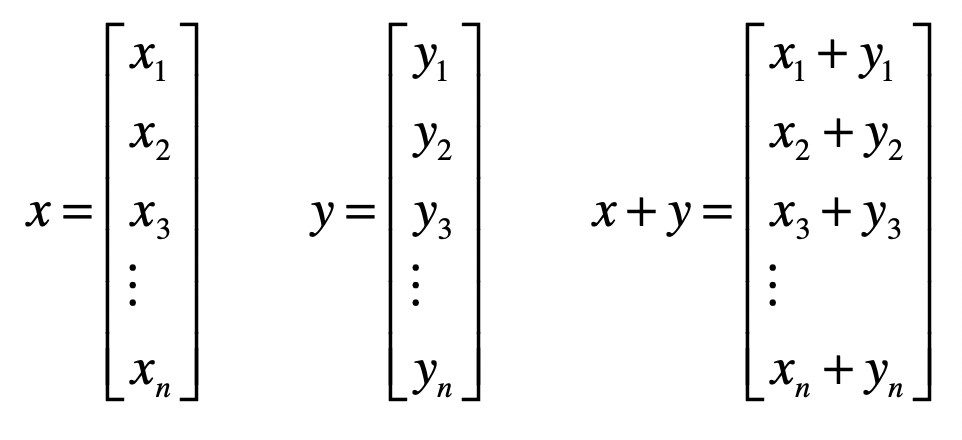
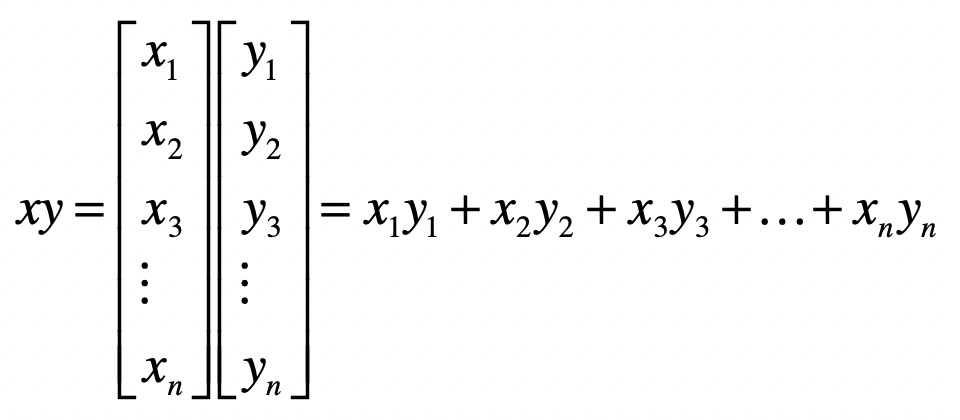
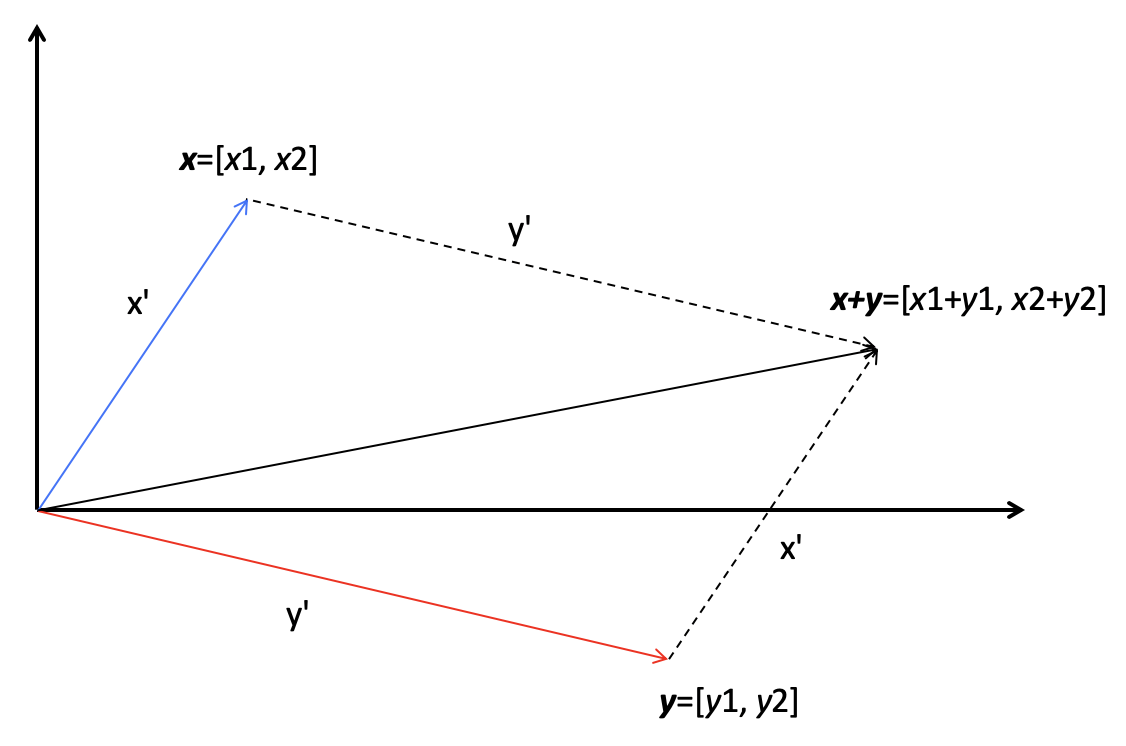
矩阵
矩阵由多个长度相等的向量组成,其中的每列或者每行就是一个向量
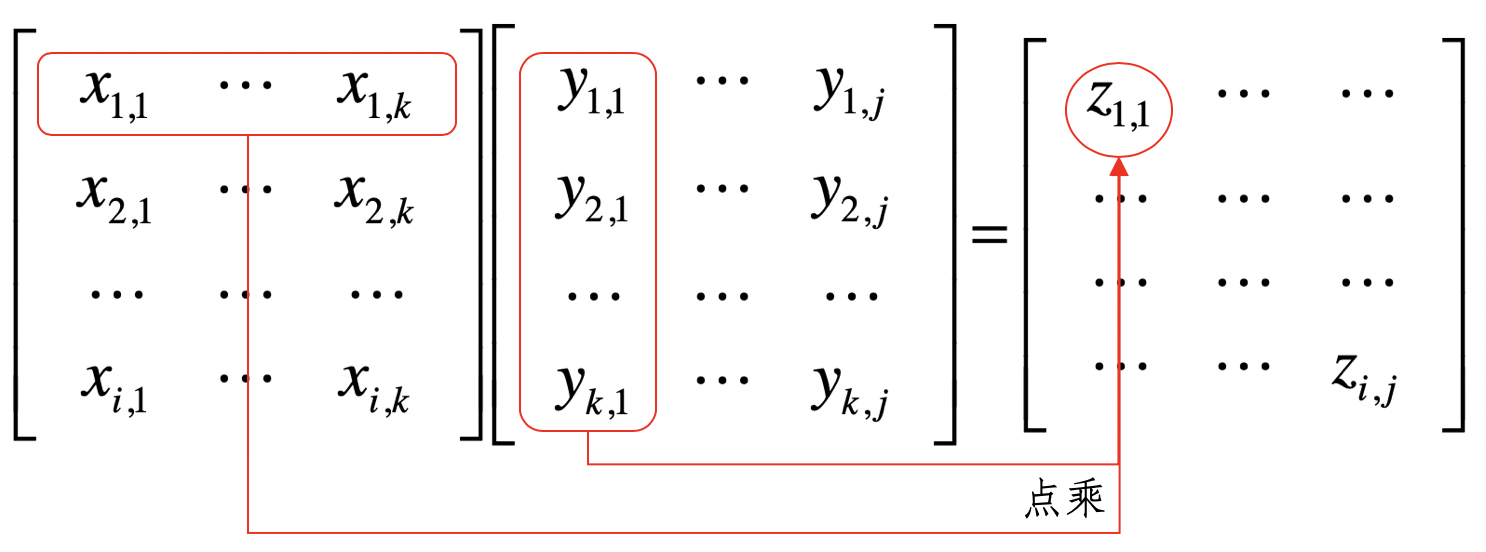
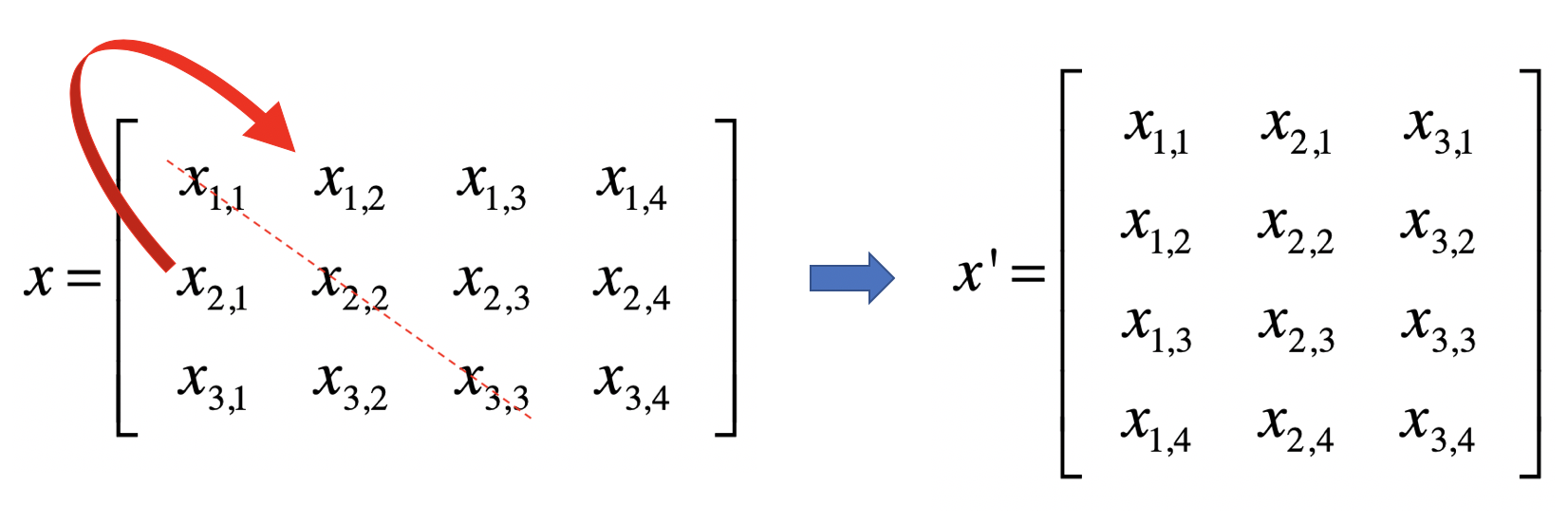
线性回归
- 当自变量 x 的个数大于 1 时就是多元回归
- 当因变量 y 个数大于 1 时就是多重回归
如果因变量和自变量为线性关系时,就是线性回归模型;如果因变量和自变量为非线性关系时,就是非线性回归分析模型
高斯消元
主要分为两步,消元(Forward Elimination)和回代(Back Substitution)
通过程式之间的运算,消除未知的x
最小二乘法
解未知参数,使得理论值与观测值之差(即误差,或者说残差)的平方和达到最小
PCA主成分分析
一种针对数值型特征、较为通用的降维方法
- 标准化样本矩阵中的原始数据;
- 获取标准化数据的协方差矩阵;
- 计算协方差矩阵的特征值和特征向量;
- 依照特征值的大小,挑选主要的特征向量;
- 生成新的特征
SVD 奇异值分解
通过样本矩阵本身的分解,找到一些“潜在的因素”,然后通过把原始的特征维度映射到较少的潜在因素之上,达到降维的目的